How Important Are GCC’s Optimization Flags – Loops

Aaron Shah | May 4, 2023 min read
How Important Are GCC’s Optimization Flags – Loops

While I was learning C++ a few years ago, I read a little about GCC’s optimization flags and how they can improve performance. I was curious about how much of a difference they actually made, so I decided to test it out.

I wrote a simple - and kinda useless, program that increments a number 2000000000 times. I compiled it with different optimization flags, and timed how long it took to run.

The Code

#include <chrono>
#include <iostream>

int test() {
    long long number = 0;
    for (long long i = 0; i != 2000000000; ++i) {
        number += 3;
    }
	std::cout << number << "\n";
    return 3;
}

template <typename T>

// you can use UNIX's time command instead, but this works for everyone.
float getExecutionTime(T f) {
    auto getTime1 = std::chrono::high_resolution_clock::now();
    f();
    auto getTime2 = std::chrono::high_resolution_clock::now();
    std::chrono::duration<double, std::milli> fpms = getTime2 - getTime1;
    return fpms.count();
}


int main() {
    std::cout << getExecutionTime(test) << "ms";
}

Results

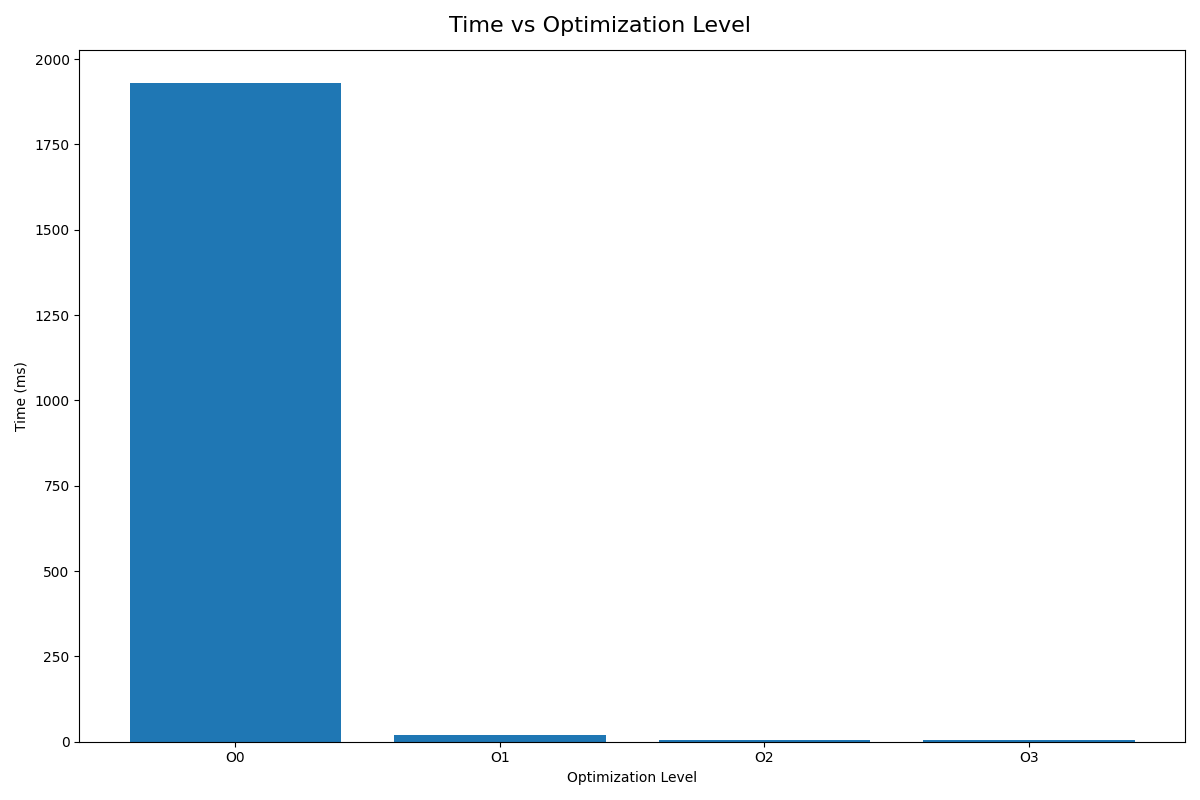
And here are the results:

Optimization Flag Time (ms)
-O0 1930
-O1 0.01966
-O2 0.005625
-O3 0.004666

As you can see, the difference is pretty significant. The program ran almost 100,000x faster with -O1 than with -O0.

So, what’s going on here? Let’s take a look at the assembly code for test() generated by GCC. I’ll be using Godbolt’s Compiler Explorer for this.

O0

test():
        push    rbp
        mov     rbp, rsp
        sub     rsp, 16
        mov     QWORD PTR [rbp-8], 0
        mov     QWORD PTR [rbp-16], 0
        jmp     .L5
.L6:
        add     QWORD PTR [rbp-8], 3
        add     QWORD PTR [rbp-16], 1
.L5:
        cmp     QWORD PTR [rbp-16], 2000000000
        jne     .L6
        mov     rax, QWORD PTR [rbp-8]
        mov     rsi, rax
        mov     edi, OFFSET FLAT:_ZSt4cout
        call    std::basic_ostream<char, std::char_traits<char> >::operator<<(long long)
        mov     esi, OFFSET FLAT:.LC0
        mov     rdi, rax
        call    std::basic_ostream<char, std::char_traits<char> >& std::operator<< <std::char_traits<char> >(std::basic_ostream<char, std::char_traits<char> >&, char const*)
        mov     eax, 3
        leave
        ret

Indeed, with no optimization, the assembly code is pretty much the same as the C++ code, with a loop that increments a number 2000000000 times.

O1

With -O1, the assembly code is much more efficient. The compiler is able to evaluate what the variable’s final value will be since it’s just a multiple of 3, and optimizes the loop away.

test():
        sub     rsp, 8
        mov     eax, 2000000000
.L2:
        sub     rax, 1
        jne     .L2
        movabs  rsi, 6000000000
        mov     edi, OFFSET FLAT:_ZSt4cout
        call    std::basic_ostream<char, std::char_traits<char> >& std::basic_ostream<char, std::char_traits<char> >::_M_insert<long long>(long long)
        mov     rdi, rax
        mov     edx, 1
        mov     esi, OFFSET FLAT:.LC0
        call    std::basic_ostream<char, std::char_traits<char> >& std::__ostream_insert<char, std::char_traits<char> >(std::basic_ostream<char, std::char_traits<char> >&, char const*, long)
        mov     eax, 3
        add     rsp, 8
        ret

O2

With -O2, the assembly code is a little cleaner, and the label for the loop is gone.

.LC0:
        .string "\n"
test():
        sub     rsp, 8
        mov     edi, OFFSET FLAT:_ZSt4cout
        movabs  rsi, 6000000000
        call    std::basic_ostream<char, std::char_traits<char> >& std::basic_ostream<char, std::char_traits<char> >::_M_insert<long long>(long long)
        mov     edx, 1
        mov     esi, OFFSET FLAT:.LC0
        mov     rdi, rax
        call    std::basic_ostream<char, std::char_traits<char> >& std::__ostream_insert<char, std::char_traits<char> >(std::basic_ostream<char, std::char_traits<char> >&, char const*, long)
        mov     eax, 3
        add     rsp, 8
        ret

There was no apparent change with -O3, but the program ran a little faster in my test anyway - maybe due to caching?

Now, this experiment doesn’t really prove anything, and won’t reflect the performance of a real program. But it does show that optimization flags can make a huge difference in performance, and that it’s worth using them.

I’ve learned that it’s best to use -O0 for testing and debugging, -O2 for emulating production tests, and -O3 for releases.

You can read more on what each optimization flag does here.

Here’s a link to all files used in this experiment: https://gist.github.com/0dm/12250a2f0e56216a54db72def97249d0

The graph was created with matplotlib.